top of page
Imaginary Numbers
Since the Babylonian period, quadratic equations, equations where the highest power of the variable "x" is 2, could be solved. During the renaissance period, Italian algebraists tackled equations of higher degrees. The group came up against a particular form of the third-degree equation. In order to get around this obstacle, one of them created the imaginary numbers. Pure thought or real extensions of real numbers?
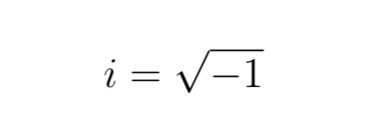
n.i.
Un nombre imaginaire
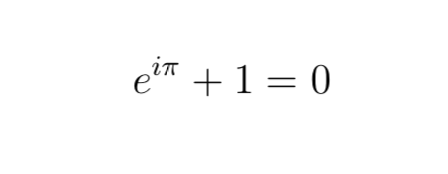
n.i.2
La formule d'Euler
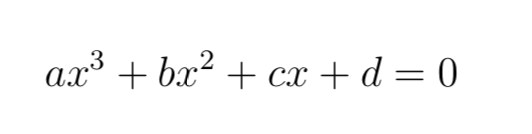
n.i.5
Les algébristes italiens essayaient de résoudre des équations de troisième degrés dont la forme générale est la suivante :
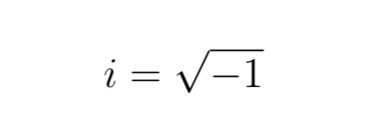
n.i.
Un nombre imaginaire
1/5
bottom of page



