top of page
Les nombres imaginaires
Depuis la période des babyloniens on pouvait résoudre des équations quadratiques, c’est-à-dire des équations dont la plus haute puissance de la variable « x » vaut 2. Durant l’époque de la renaissance, les algébristes italiens s’attaquent aux équations de degrés supérieurs. Ces derniers se butent à une forme particulière de l’équation du troisième degré et afin de contourner cet obstacle, l’un d’entre eux crée les nombres imaginaires... Pur fruit de la pensée ou véritables prolongement des nombres réels ?
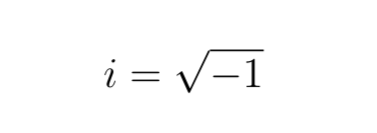
n.i.
Un nombre imaginaire
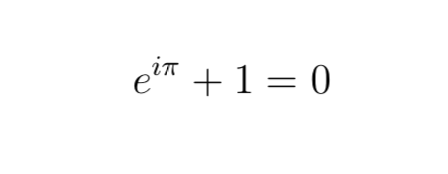
n.i.2
La formule d'Euler
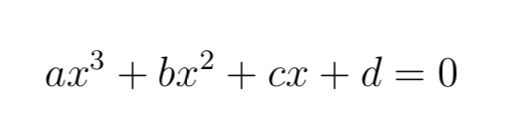
n.i.5
Les algébristes italiens essayaient de résoudre des équations de troisième degrés dont la forme générale est la suivante :
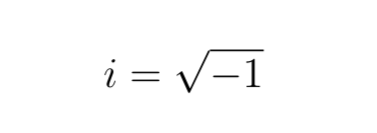
n.i.
Un nombre imaginaire
1/5
bottom of page



